提问于:
浏览数:
4093
```tex
\documentclass[12pt,a4]{article}
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
\usepackage{amsfonts}
\usepackage{amsthm}
\usepackage{amsmath,mathrsfs}
\usepackage{amssymb}
\usepackage{graphicx}
\usepackage{subfig}
\usepackage{cite}
\setcounter{MaxMatrixCols}{10}
%TCIDATA{OutputFilter=LATEX.DLL}
%TCIDATA{Version=5.00.0.2606}
%TCIDATA{}
%TCIDATA{BibliographyScheme=Manual}
%TCIDATA{LastRevised=Monday, April 29, 2013 16:28:32}
%TCIDATA{}
%TCIDATA{Language=American English}
\topmargin -0.5cm \oddsidemargin -0.5cm \evensidemargin -0.5cm
\textwidth=17 true cm \textheight=23.2 true cm
%\input{tcilatex}
\begin{document}
\title{ Parallel *** in Hilbert space }
\author{*** $^{1,}$\thanks{Corresponding author.}, ??? $^2$
\\
\\
\footnotesize{$^1$ Department of Mathematics, ***
University}\\
\footnotesize{ ***, China}\\
\footnotesize{ $^2$ Department of Engineering, *** University}\\
\footnotesize{ ***, China}\\
\\
\\
\\ \footnotesize{ E-mails: ???@163l.com}
}
\date{}
\maketitle
{\footnotesize \noindent \textbf{Abstract.} \vskip 0.2cm }
{\footnotesize \noindent \textbf{Keywords}: .\vskip 1mm }
{\footnotesize \noindent \textbf{2010 AMS Subject Classification}: }
\vskip 4mm
\section*{1. Introduction}
\vskip 0.5cm
\section*{2. Preliminaries}\vskip 2mm
\section*{3. Main results}
\vskip0.3cm
\newpage
where $\{\alpha_n\}\subset(0,1)$, $\rho\in(0,\min\{\frac{1}{2c_1},\frac{1}{2c_2}\}$. If $\lim_{n\to\infty}\alpha_n=0$, then $\{x_n\}$ generated by $(3.20)$ converges strongly to element $\hat{x}=P_\Omega x_1.$
\vskip0.2cm
\noindent
{\bf Remark 3.2} If $U_i\equiv U$ for each $i=1,\ldots, N$ and $V_j\equiv V$ for each $j=1,\ldots, M$ in Theorems 3.1 and 3.2, we obtain the corresponding results announced in \cite[Theorem 1,Theorem 2]{HieuMuuAnh2016}.
\vskip0.2cm
\section*{4. Numerical experiment}
\vskip0.2cm
In this section, we give an example to illustrate the algorithms in this paper. We perform the algorithms by Matlab R2008a running on a PC Desktop with Core(TM) i3CPU M550 3.20GHz with 4GB Ram.
\vskip0.2cm
\noindent
{\bf Example 4.1} Let $H=\mathbb{R}^3$ and $U_1=\{(x_1,x_2,x_3): x_1\in[0,1], x_2\geq 0,x_3\geq 0\}$, $U_2=\{(x_1,x_2,x_3): x_1\geq 0,x_2\in[0,2], x_3\geq 0\}$ and $U_3=\{(x_1,x_2,x_3): x_1\geq 0,x_2\geq 0, x_3\in[0,3]\}$. For each $i=1,2,3$, let $f_i(x,y)=(y_i-x_i)\|x\|$ for all $x=(x_1,x_2,x_3), y=(y_1,y_2,y_3)\in U_i$. From \cite{Wang2018} it follows that each $f_i$ satisfies the conditions (i)-(iv) with the Lipschitz constants $c_1=c_2=1$.
Let $V_j=\{(x_1,x_2,x_3): x_1\in\mathbb{R}, 0\leq x_2\leq j,x_3\geq 0\}$ for each $j=1,\ldots,M$. Define the nonexpansive mapping $S_j$ on $V_j$ by $S_jx=(-\frac{x_1}{2}, \frac{x_2^2}{6j},\frac{x_3}{2})$ for $j=1,\ldots,M$. Obviously, $\mathcal{F}=\cap_{i=1}^3 EP(f_i)\cap(\cap_{j=1}^M)Fix(S_j)=\{(0,0,0)\}$.
In Algorithm 3.1 and 3.2, put the sequence
$\alpha_n=\frac{1}{10}$ and $\alpha_n=\frac{1}{n}$, respectively and put $\rho=\frac{1}{4}$ and $\beta_n= 0.8(1-0.8 e^{-\frac{n}{10}})$ in Algorithm 3.1 and 3.2. According to Theorem 3.1 and 3.2, the sequence $\{x_n\}$ generated by Algorithm 3.1 and 3.2 will converge to the element $x^*=P_{\mathcal{F}}x_1=(0,0,0)$. We will stop the program if $\|x_n\|<10^{-4}$.
The following figures show the convergence of Algorithm 3.1 and 3.2 with the different initial point.
\begin{figure}[h]
\centering
\subfloat {%
\includegraphics[width=5.2in,totalheight=3.9in]{a1.eps}}\
\caption{ Convergence of Algorithm 3.1 and 3.2 with initial point $x_1=(3,2,10)$}
\end{figure}
\iffalse
\section*{Acknowledgments}
\vskip0.2cm
This work is supported by Natural Science Foundation of Hebei Province (N0. A2015502021) and the Fundamental Research Funds for the Central Universities (No. 2015MS78).
\fi
\begin{thebibliography}{99}
\setlength{\itemsep}{-0.02cm}
\bibitem{Anh2013}P.N. Anh, A hybrid extragradient method extended to fixed point problems and equilibrium problems, Optimization, 63, (2013) 271--283.
\bibitem{Anh2013-2}P.N. Anh, A hybrid extragradient method for pseudomonotone equilibrium problems and fixed point problems, Bull. Malays. Math. Sci. 36 (2013) 107--116.
\bibitem{AhnThi2013}P.N. Anh, H.A. Le Thi, An Armijo-type method for pseudomonotone equilibrium problems and its applications, J. Glob. Optim. 57 (2013) 803--820.
%\bibitem{Bnouhachem2014}A. Bnouhachem, Strong convergence algorithm for split equilibrium problems and hierarchical fixed point problems, The Scientific World Journal, 2014, Article ID 390956, 12 pages.
%\bibitem{Ceng2008}L.C. Ceng, P. Cubiotti, J.C. Yao, {\it An implicit iterative scheme for monotone variational inequalities and fixed point problems},
% Nonlinear Anal., {\bf69}, (2008), 2445--2457.
% \bibitem{CensorBibaliReich2012}Y. Censor, A. Gibali, S. Reich, Algorithms for the split variational inequality problem, Number Algor. 59 (2012) 301--323
\bibitem{ChangLeeChan2009}S.-S. Chang, H. W. J. Lee, and C. K. Chan, A new method for
solving equilibrium problem fixed point problem and variational inequality problem with application to optimization,
Nonlinear Analysis, Theory, Methods and Applications, 70 (2009) 3307--3319.
%\bibitem{ChoZhou2004}Y. J. Cho, H.Y. Zhou and G.T. Guo, Weak and strong convergence theorems for three-step iterations with errors for asymptotically nonexpansive mappings, Comput. Math. Appl. 47 (2004) 707--717.
\bibitem{CombettesHirstoaga1997}P. L. Combettes, S. A. Hirstoaga, Equilibrium programming
using proximal like algorithms, Mathematical Prog.
78 (1997) 29--41.
\bibitem{CombettesHirstoaga2005}P.L. Combettes, S.A. Hirstoaga, Equilibrium
programming in Hiblert spaces, J. Nonlinear Convex Anal. 6 (2005) 117--136.
\bibitem{DinhMuu2015}B.V. Dinh, L. D. Muu, A projection algorithm for solving pseudomonotone equilibrium problems and its application to a class of bilievel equilibria, Optimization. 64 (2015) 559--575.
\bibitem{DinhKim2016}B. V. Dinh, D.S. Kim, Projection algorithms for solving nonmonotone equilibrium problems in Hilbert space, J. Comput. Appl. Math. 302 (2016) 106--117
\bibitem{FacchineiPang2003}F. Facchinei, J.S. Pang, Finite-dimensional variational inequalities and complementary problems, Springer-Verlag, New York, 2003.
% \bibitem{FangHuang2003}Y.P. Fang, N.J. Huang, Variational-like inequilities with generalized
%monotone mappings in Banach spaces, J. Optim. Theory Appl. 118 (2003) 327--338.
\bibitem{HieuMuuAnh2016}D.V. Hieu, L. D. Muu, P.K. Anh, Parallel hybrid extragradient methods for pseudomotone equilibrium problems and nonexpansive mappings, Numer Algor 73 (2016) 197--217.
%\bibitem{IidukaTakahashi2005} H. Iiduka, W. Takahashi, Strong convergence theorems for nonexpansive mappings and inverse-strongly monotone mappings, Nonlinear Anal. (61) (2005) 341--350.
\bibitem{KangChoLiu2010}S.M. Kang, S.Y. Cho, Z. Liu, Convergence of iterative sequences for generalized equilibrium problems involving
inverse-strongly monotone mappings. J. Inequal. Appl. 2010, 827082 (2010)
\bibitem{KatchangKumam2010} P. Katchang and P. Kumam, A new iterative algorithm of solution
for equilibriumproblems, variational inequalities and fixed point problems in a Hilbert space, Journal of Applied Mathematics
and Computing, 32 (2010) 19--38.
%\bibitem{KazmiRizvi2013}K. R. Kazmi and S. H. Rizvi, Iterative approximation of a
%common solution of a split equilibrium problem, a variational
%inequality problem and a fixed point problem, Journal of the
%Egyptian Math. Society 21 (2013) 44--51.
%\bibitem{Liu1995} L.S. Liu, Iterative processes with errors for nonlinear strongly accretive mappings in Banach spaces, J. Math. Anal.%
%Appl. 194 (1995) 114--125.
%\bibitem{Mainge2007} P.E. Maing\'{e}, Approximation methods for common fixed points of nonexpansive mappings in Hilbert spaces, J. Math. Anal. Appl. vol. 325 (2007), 469--479.
\bibitem{Mainge2008} P.E. Maing\'{e}, Strong convergence of projected subgradient methods for nonsmooth and nonstrictly convex minimization, Set-Valued Anal. 16 (2008) 899--912.
%\bibitem{Moudafi2011} A. Moudafi, Split Monotone Variational Inclusions, J. Optim Theory
%Appl. 150 (2011) 275--283.
\bibitem{PlubtiengPunpaeng2007} S. Plubtieng and R. Punpaeng, A general iterative method
for equilibrium problems and fixed point problems in Hilbert
spaces, J. Math. Anal. Appl.
336 (2007) 455--469.
\bibitem{QinChoKang2010}X. Qin, Y.J. Cho, S.M. Kang, Viscosity approximation methods for
generalized equilibrium problems and fixed point
problems with applications. Nonlinear Anal. 72, 99--112 (2010)
\bibitem{QinShangSu2008} X. Qin, M. Shang, and Y. Su, A general iterative method
for equilibrium problems and fixed point problems in Hilbert
spaces, Nonlinear Anal.
69 (2008) 3897--3909.
% \bibitem{Suzuki2005}T. Suzuki, Strong convergence of Krasnoselskii and Mann's type sequences for one-parameter nonexpansive semigroups without Bochner integrals, J. Math. Anal. Appl. 305 (2005) 227--239.
% \bibitem{Takahashi2000}W. Takahashi, Nonlinear Functional Analysis, Yokohama Publishers, Yokohama, 2000.
\end{thebibliography}
\end{document}
```
希望插入的图片在参考文献和The following figures show the 。。之间,也就是图片1中黑色箭头位置,但编译完后却出现在图2位置, 代码处已经添加了参数h了。图a1.esp 不知道怎么上传。只上传了图1和2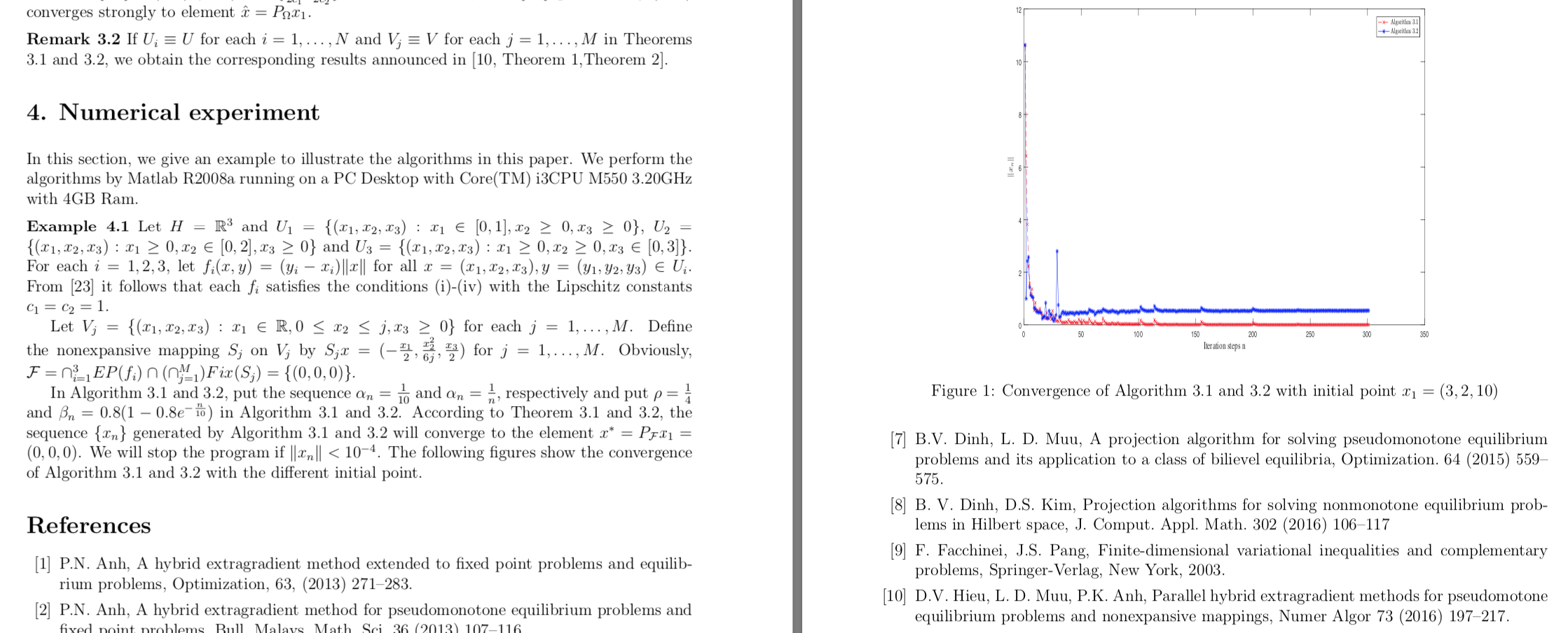
4 回答
0
怎么上传完问题变成这个效果了。
在哪里写代码,哪里写具体问题,如何上传.esp图片呢,没闹明白。
0
插图如果用了
```tex
\begin{figure}
...
\end{figure}
```
那么你就启用了浮动体。
浮动体就是让系统自己决定图片在什么位置最合适,所以你不用管它。
0
你的那个位置放不下图片才浮动的.
你可以缩小图片, 适配空余的空间就好了.
0
浮动体就是为了防止当插图大小不合适时,采用固定位置造成的**留白**的,应该相信LaTeX能够很好的处理浮动体。
如果觉得不爽,有两种方案:一是缩放插图到合适大小。二是精简文字留出地方或是添加废话把插图“挤到”下一页。
如果缩小后清晰度和字号等影响过大,那么就采用第2方案吧,精简和添加废话对能写论文的人来讲,都不是个事。
其实,完全可以不用太操心这些,有交叉引用,读者知道去哪里找这个插图。
你的回答
请登录后回答
你的回答将会帮助更多人,请务必认真回答问题。
