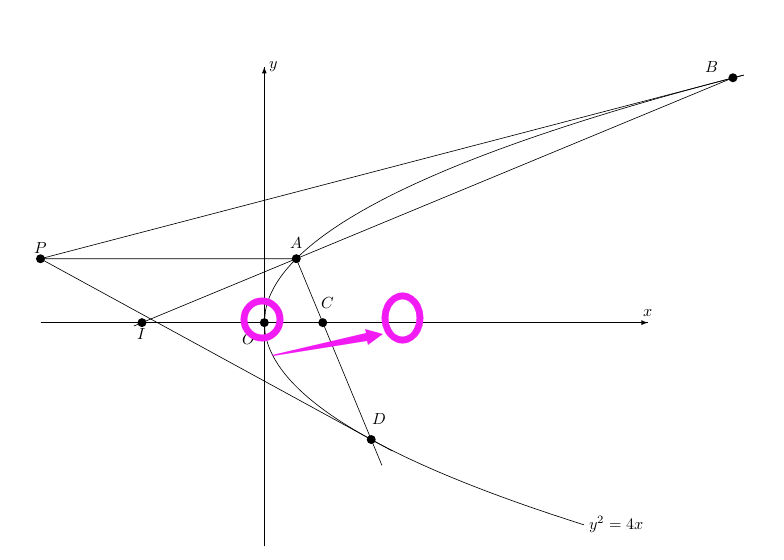
如下图，C 点是以「交点」的方式求得的，并不知其确切坐标，欲作原点(0,0) 关于 点 C 对称的点Q，也即是在 x 轴上找一点Q，令OC=CQ，求问如何引用『线短OC之长』？  ```lua $$\begin{tikzpicture}[scale=0.7] \draw[-latex] (-7,0) -- (12,0) node [above]{$x$}; \draw[-latex] (0,-7) -- (0,8) node [right]{$y$}; \draw plot[samples=400,domain=0:15](\x,{2*sqrt(\x)}) ; \draw[name path=a,yscale=-1] plot[samples=400,domain=0:10](\x,{2*sqrt(\x)}) node[right]{$y^2=4{x}$}; \coordinate(A) at(1,2); \coordinate(B) at(14.66,7.66); \draw[name path=f](A)--(B); \coordinate (Q) at ($(A)!-7cm!90:(B)$); \draw [name path=b](Q)--(A); \draw[name path=o] (-7,0) -- (12,0) ; \draw[name path=t] (0,-7) -- (0,8); \fill [name intersections={of=a and b, by={D}}] (D) circle (4pt) node at (3.6,-3) {$D$}; \draw[name path=c,domain=-7:4] plot(\x,{(-2*\x-6.69)/3.66}); \draw[name path=d,domain=-7:15] plot(\x,{(2*\x+29.31)/7.66}) ; \fill [name intersections={of=c and d, by={P}}] (P) circle (4pt) node[above] {$P$}; \fill [name intersections={of=o and b, by={C}}] (C) circle (4pt) node at (2,.6) {$C$}; \fill (A) circle (4pt) node at (1,2.5) {$A$}; \fill (B) circle (4pt) node at (14,8) {$B$}; \fill (0,0) circle (4pt) node at (-0.5,-0.5) {$O$}; \draw[name path=g](P)--(A); \coordinate (W) at ($(A)!-5.5cm!(B)$); \draw [name path=w](A)--(W); \fill [name intersections={of=o and w, by={I}}] (I) circle (4pt) node[below] {$I$}; \end{tikzpicture}$$ ```