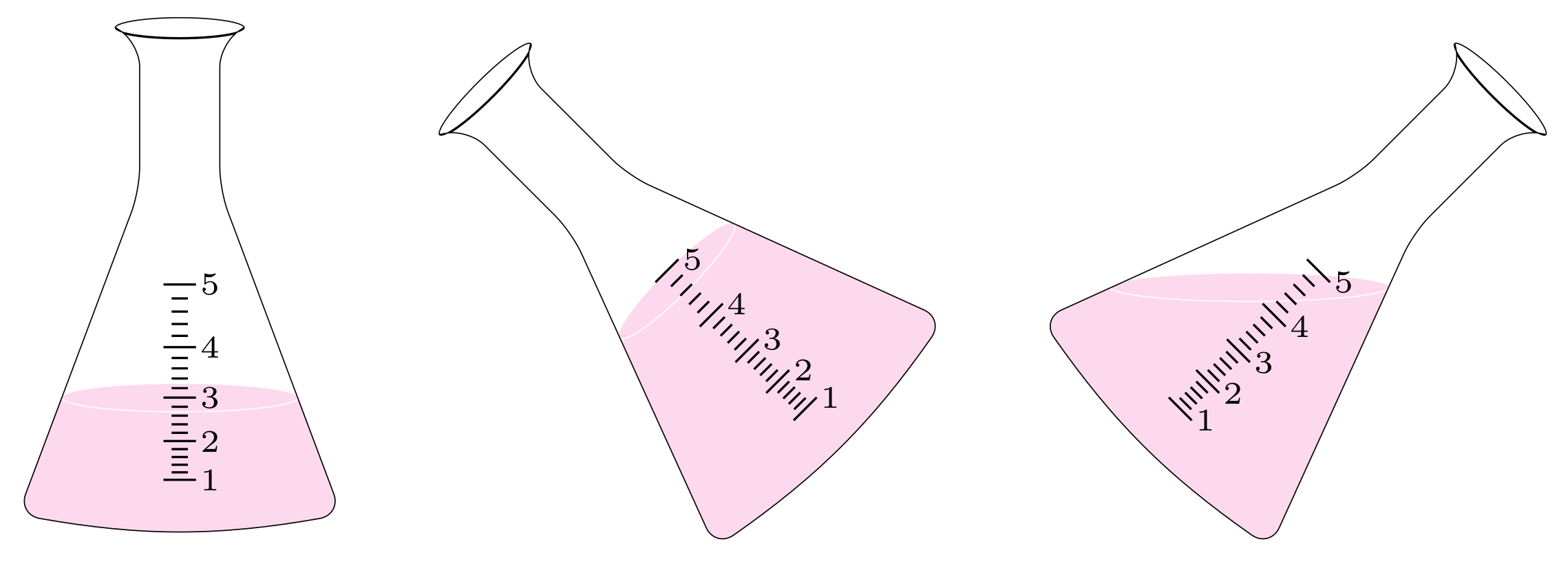
最近想用TikZ画一下化学中的一些器材,通过参考latex-glassware和tikz-labo实现了试管、烧瓶等的绘制。
现有一个疑惑,当给scope传入rotate旋转参数后,也会造成液面的统一旋转,从而无法保持液面的水平状态。
一个简单的想法是在scope内能取得传入rotate旋转角度,然后对溶液和液面椭圆进行反向旋转。
为验证想法,用45度进行了测试,反旋转可以实现液面保持水平。
但是,没有找到如何在scope内获取rotate旋转角度的方法,各位网友可否指点一二?
目前的绘制结果为:
实现的MWE为:
\documentclass[margin=3pt,
convert,
convert={
outext=.png,
command=\unexpanded{
pdftocairo -r 600 -png \infile % 将生成的pdf文件转换为png图像
}
}
]{standalone}
\usepackage{ctex}
\usepackage{ifthen}
\newcommand{\ifnonzero}[2]{
\ifthenelse{\equal{#1}{0}}{}{#2}
}
% \usepackage{calc}
\usepackage{tikz}
\usetikzlibrary{calc}
\usetikzlibrary{intersections}
% 烧瓶
% 根据梯形面积等分刻度
% 用定积分法计算等分线:
% 瓶底半径:1
% 瓶口半径:0.25
% 高度:2(不含颈部)
% 顺时针转90度,用两点公式写出直线方程:y=(-3/8)*x + 1
% 求积分:(-3/16)*x*x + x
% 0-2定积分得总面积为:5/4
% 根据传入的#3比例参数,确定当前面积为:#3 * 5 / 4
% 解方程:(-3/16)*x*x + x - #3 * 5 / 4 = 0
% 可得用于绘制的液面高度
\newcommand{\flask}[3][]{
\begin{scope}[shift={(#2)},glassware,#1]
% 方程系数
\pgfmathsetmacro{\a}{-3/16}
\pgfmathsetmacro{\b}{1}
\pgfmathsetmacro{\m}{-1 * \b / (2 * \a)}
% 液面系数为不0
\ifnonzero{#3}{
% 烧瓶外框路径,并构成裁剪区域
\clip[rounded corners, name path = P1] (-0.4, 3)--++(0.15,-0.1)
--++(0,-0.9)--++(-0.75, -2.0)to[bend right=10pt]++(2.0, 0.0)--++(-0.75, 2.0)
--++(0.0, 0.9)--++(0.15, 0.10)
++(-0.4, 0.0) circle [x radius=0.4, y radius=0.065]--cycle;%
% 计算液面高度
\pgfmathsetmacro{\c}{-1 * #3 * 5 / 4}
\pgfmathsetmacro{\delta}{\b * \b - 4 * \a * \c}
\pgfmathsetmacro{\n}{sqrt(abs(\delta)) / (2 * abs(\a))}
\pgfmathsetmacro{\i}{\m - \n}
% 绘制液面矩形并被烧瓶裁剪
% TODO:如何获得给scope转入的rotate旋转参数
% 从而进行反旋转以保持液面水平?
\fill[name path=P2] (-1.0, -3.5pt) rectangle (1.0, \i);
% 绘制液面椭圆标志
% 求交点
\path [name intersections={of=P1 and P2, by={E,F}}];
% 计算中点
\node (M) at ($(E)!0.5!(F)$){};
% 计算半径并绘制液面椭圆标志
\fill[draw=white, very thin] (E) let \p1 = ($(M)-(E)$),
\n2 = {veclen(\x1,\y1)}
in ++(\n2, 0) circle[x radius = \n2, y radius = 2.5pt];
}
% 绘制刻度线(用积分法计算出刻度位置)
\pgfmathtruncatemacro{\lticklable}{1}
% 计算刻度位置
\pgfmathsetmacro{\c}{-1 * 5 / 24}
\pgfmathsetmacro{\delta}{\b * \b - 4 * \a * \c}
\pgfmathsetmacro{\n}{sqrt(abs(\delta)) / (2 * abs(\a))}
\pgfmathsetmacro{\i}{\m - \n}
% 多带带处理第1个坐标刻度,以便在循环中可以处理大刻度(mod 5运算)
\draw (-0.1, \i)--(0.1, \i) node[right, xshift=-3pt](\lticklable){\tiny{}\lticklable};
\foreach \y[count=\x] in {6,7,...,25}% 刻度位置占有单位面积数
{
\pgfmathsetmacro{\c}{-1 * \y / 24}
\pgfmathsetmacro{\delta}{\b * \b - 4 * \a * \c}
\pgfmathsetmacro{\n}{sqrt(abs(\delta)) / (2 * abs(\a))}
\pgfmathsetmacro{\i}{\m - \n}
\pgfmathtruncatemacro{\ltick}{mod(\x, 5)}
\ifnum\ltick=0
\pgfmathtruncatemacro{\lticklable}{\x / 5 + 1}
\draw (-0.1,\i)--(0.1,\i) node[right, xshift=-3pt](\lticklable){\tiny{}\lticklable};
\else
\draw (-0.05,\i)--(0.05,\i);
\fi
}
% 绘制烧瓶外框
\draw[rounded corners] (-0.4, 3)--++(0.15,-0.1)
--++(0,-0.9)--++(-0.75, -2.0)to[bend right=10pt]++(2.0, 0.0)--++(-0.75, 2.0)
--++(0.0, 0.9)--++(0.15, 0.10)
++(-0.4, 0.0) circle [x radius=0.4, y radius=0.065]--cycle;%
\end{scope}
}
\newcommand{\iflask}[3][]{
\begin{scope}[shift={(#2)},glassware,#1]
% 方程系数
\pgfmathsetmacro{\a}{-3/16}
\pgfmathsetmacro{\b}{1}
\pgfmathsetmacro{\m}{-1 * \b / (2 * \a)}
% 液面系数为不0
\ifnonzero{#3}{
% 烧瓶外框路径,并构成裁剪区域
\clip[rounded corners, name path = P1] (-0.4, 3)--++(0.15,-0.1)
--++(0,-0.9)--++(-0.75, -2.0)to[bend right=10pt]++(2.0, 0.0)--++(-0.75, 2.0)
--++(0.0, 0.9)--++(0.15, 0.10)
++(-0.4, 0.0) circle [x radius=0.4, y radius=0.065]--cycle;%
% 计算液面高度
\pgfmathsetmacro{\c}{-1 * #3 * 5 / 4}
\pgfmathsetmacro{\delta}{\b * \b - 4 * \a * \c}
\pgfmathsetmacro{\n}{sqrt(abs(\delta)) / (2 * abs(\a))}
\pgfmathsetmacro{\i}{\m - \n}
% 绘制液面矩形并被烧瓶裁剪
% 旋转
\fill[rotate=45,name path=P2] (-3.0, -25pt) rectangle (3.0, \i);
% 绘制液面椭圆标志
% 反向旋转45度
\path [name intersections={of=P1 and P2, by={E,F}}];
% 计算中点
\node (M) at ($(E)!0.5!(F)$){};
% 计算半径并绘制液面椭圆标志
% 反向旋转45度
\fill[rotate = 45, draw=white, very thin] (E) let \p1 = ($(M)-(E)$),
\n2 = {veclen(\x1,\y1)}
in ++(\n2, 0) circle[x radius = \n2, y radius = 2.5pt];
}
% 绘制刻度线(用积分法计算出刻度位置)
\pgfmathtruncatemacro{\lticklable}{1}
% 计算刻度位置
\pgfmathsetmacro{\c}{-1 * 5 / 24}
\pgfmathsetmacro{\delta}{\b * \b - 4 * \a * \c}
\pgfmathsetmacro{\n}{sqrt(abs(\delta)) / (2 * abs(\a))}
\pgfmathsetmacro{\i}{\m - \n}
% 多带带处理第1个坐标刻度,以便在循环中可以处理大刻度(mod 5运算)
\draw (-0.1, \i)--(0.1, \i) node[right, xshift=-3pt](\lticklable){\tiny{}\lticklable};
\foreach \y[count=\x] in {6,7,...,25}% 刻度位置占有单位面积数
{
\pgfmathsetmacro{\c}{-1 * \y / 24}
\pgfmathsetmacro{\delta}{\b * \b - 4 * \a * \c}
\pgfmathsetmacro{\n}{sqrt(abs(\delta)) / (2 * abs(\a))}
\pgfmathsetmacro{\i}{\m - \n}
\pgfmathtruncatemacro{\ltick}{mod(\x, 5)}
\ifnum\ltick=0
\pgfmathtruncatemacro{\lticklable}{\x / 5 + 1}
\draw (-0.1,\i)--(0.1,\i) node[right, xshift=-3pt](\lticklable){\tiny{}\lticklable};
\else
\draw (-0.05,\i)--(0.05,\i);
\fi
}
% 绘制烧瓶外框
\draw[rounded corners] (-0.4, 3)--++(0.15,-0.1)
--++(0,-0.9)--++(-0.75, -2.0)to[bend right=10pt]++(2.0, 0.0)--++(-0.75, 2.0)
--++(0.0, 0.9)--++(0.15, 0.10)
++(-0.4, 0.0) circle [x radius=0.4, y radius=0.065]--cycle;%
\end{scope}
}
\begin{document}
\begin{tikzpicture}
\tikzstyle{glassware} = [fill=magenta!15]
\flask{0,0}{0.50}
\flask[rotate=45]{4,0.5}{0.80}
\iflask[rotate=-45]{6,0.5}{0.60}
\end{tikzpicture}
\end{document}